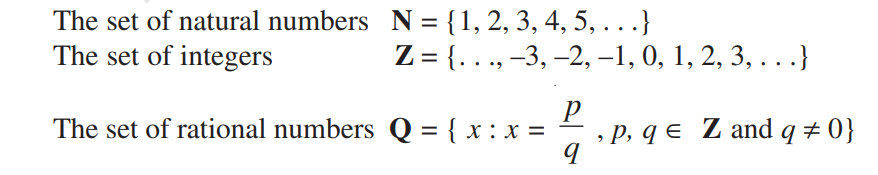




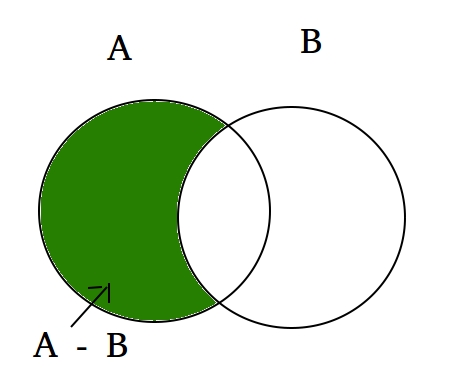
Given two non-empty sets P and Q. The cartesian product P × Q is the set of all ordered pairs of
elements from P and Q, i.e.,
P × Q = { (p,q) : p ∈ P, q ∈ Q }
eg : A= {a1, a2} and B = {b1, b2, b3, b4}
then
A × B = {( a1, b1), (a1, b2), (a1, b3), (a1, b4), (a2, b1), (a2, b2), (a2, b3), (a2, b4)}
Remarks
(i) Two ordered pairs are equal, if and only if the corresponding first elements are equal and
the second elements are also equal
(ii) If there are p elements in A and q elements in B, then there will be pq elements in A × B,
i.e., if n(A) = p and n(B) = q, then n(A × B) = pq.
(iii) If A and B are non-empty sets and
either A or B is an infinite set, then so is A × B.
(iv) A × A × A = {(a, b, c) : a, b, c ∈
A}.
Here (a, b, c) is called an ordered triplet.
| Relations |
|---|
| A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product A × B. |
| The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in A × B. The second element is called the image of the first element. |
| The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R. |
| The set of all second elements in a relation R from a set A to a set B is called the range of the relation R. The whole set B is called the codomain of the relation R. Note that range ⊂ codomain |
| Operations in Relation | |
|---|---|
| intersection | R
∩
S
=
{
(
a
,
b
)
∣
a
R
b
and
a
S
b
}
,
where a ∈ A and b ∈ B . |
| Union | R
∪
S
=
{
(
a
,
b
)
∣
a
R
b
or
a
S
b
}
,
provided a ∈ A and b ∈ B . |
| Difference | R
∖
S
=
{
(
a
,
b
)
∣
a
R
b
and not
a
S
b
}
,
S ∖ R = { ( a , b ) ∣ a S b and not a R b } |
| Functions |
|---|
| special type of relation called function |
| A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B. |
| In other words, a function f is a relation from a non-empty set A to a non-empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element. |
| If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f. |
| The function f from A to B is denoted by f: A à B. |
| eg : Let N be the set of natural numbers and the relation R be defined on N such that R = {(x, y) : y = 2x, x, y ∈ N} |
| Relations Types | Definitions |
|---|---|
| EMPTY | If no element of set X is related or mapped to any element of X, then the
relation R in A is an empty relation, i.e, R = Φ. Think of an example of set A consisting of only 100 hens in a poultry farm. Is there any possibility of finding a relation R of getting any elephant in the farm? No! R is a void or empty relation since there are only 100 hens and no elephant. |
| UNIVERSAL | A relation R in a set, say A is a universal relation if each element of A is
related to every element of A, i.e., R = A × A. Also called Full relation.
Suppose A is a set of all natural numbers and B is a set of all whole numbers. The relation between A and B is universal as every element of A is in set B. Empty relation and Universal relation are sometimes called trivial relation. |
| IDENTITY | In Identity relation, every element of set A is related to itself only. I = {(a,
a), ∈ A}. For example, If we throw two dice, we get 36 possible outcomes, (1, 1), (1, 2), … , (6, 6). If we define a relation as R: {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}, it is an identity relation. |
| INVERSE | Let R be a relation from set A to set B i.e., R ∈ A × B. The relation R-1 is
said to be an Inverse relation if R-1 from set B to A is denoted by R-1 = {(b,
a): (a, b) ∈ R}. Considering the case of throwing of two dice if R = {(1, 2), (2, 3)}, R-1 = {(2, 1), (3, 2)}. Here, the domain of R is the range of R-1 and vice-versa. |
| REFLEXIVE | If every element of set A maps to itself, the relation is Reflexive Relation. For every a ∈ A, (a, a) ∈ R. |
| IRREFLEXIVE | Relation R on a set A is irreflexive if (a,a) not element of R for all a ∈ A |
| A relation can be reflexive or irreflexive or neither | |
| SYMMETRIC | A relation R on a set A is said to be symmetric if (a, b) ∈ R then (b, a) ∈ R, for all a & b ∈ A. |
| ANTI-SYMMETRIC | R is ANTI-SYMMETRIC if xRY & yRx implies x=y for all x,y ∈ A , ie if xRy then y(not)Rx for all pairs where there is a relation |
| A relation can be symmetric or antisymmetric or neither | |
| TRANSITIVE | A relation in a set A is transitive if, (a, b) ∈ R, (b, c) ∈ R, then (a, c) ∈ R, for all a, b, c ∈ A |
| EQUIVALENCE | A relation is said to be equivalence if and only if it is Reflexive, Symmetric, and Transitive. For example, if we throw two dices A & B and note down all the possible outcome. |
| PARTIAL ORDER | A relation R on set A is called a partial ordering or partial order if it is reflexive, anti-symmetric and transitive. A set A together with a partial ordering R is called a partially ordered set or poset. The poset is denoted as (S,R). |
| VOID | We can define void relation as a relation R in a set A, where no element of set A is related to any element of A. So, R = ɸ which is a subset of A × A. |
Q : Are all functions relations?
A function is a kind of interrelationship among objects. Moreover, a function defines a set of
finite lists of objects, one for each combination of possible arguments. Besides, a relation is
another kind of interrelationship among object in the world of discourse. Furthermore, both
function and relation are defined as a set of lists. And
every function is a relation but not
every relation is a function.
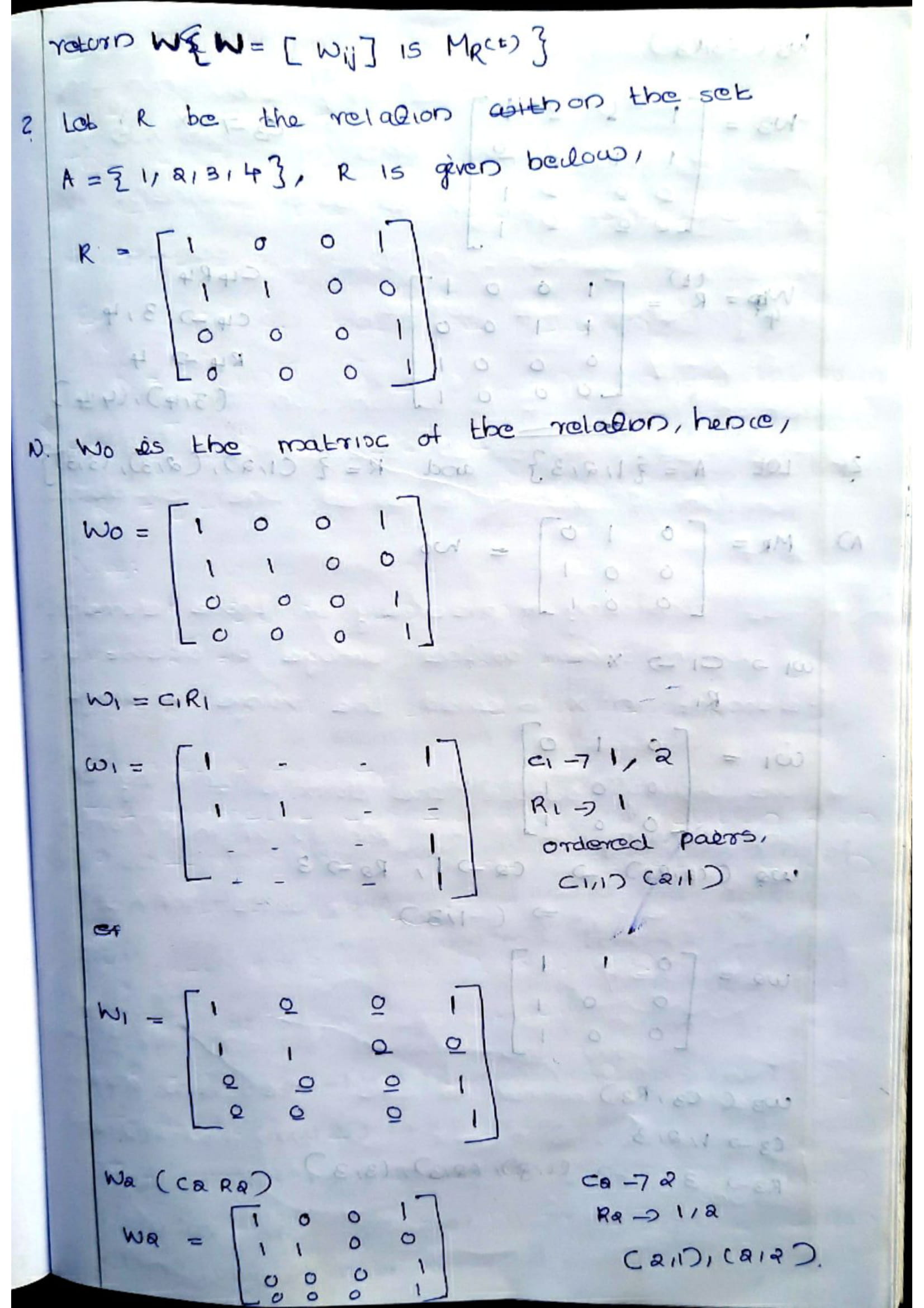
x Relation as Matrices:
A relation R is defined as from set A to set B,then the matrix representation of relation is
MR=
[mij ]
where
mij = { 1, if (a,b) Є R;
0, if (a,b) Є R }

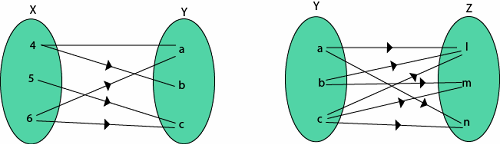
Let X = {4, 5, 6}, Y = {a, b, c} and Z = {l, m, n}. Consider the relation R1 from X to Y and R2
from Y to Z
then ..
R1 = {(4, a), (4, b), (5, c), (6, a), (6, c)}
R2 = {(a, l), (a, n), (b, l), (b, m), (c, l), (c, m), (c, n)}
.png)